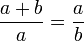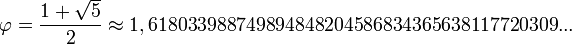Actividad 1.3

Funciones Trigonométricas

5)

Teorema de Pitágoras

1.- Un triángulo rectángulo está inscrito en una semicircunferencia con diámetro igual a 50. Uno de los catetos del triángulo rectángulo mide 35. Determina las dimensiones del triángulo rectángulo.

2.- Construye un triángulo rectángulo cuyos catetos miden CM= 60 , Cm= 45. Trazar el triángulo y la semicircunferencia circunscrita. 

Actividad 1.2 "Áreas y volúmenes"

Problemas de razonamiento

• La siguiente figura es el plano de un área recreativa que se va a construir al oriente de la ciudad. Tiene la forma de un cuadrado de área igual a 4900 m². El semicírculo de la derecha está destinado a una alberca con área de regaderas y espacios para tomar el sol; las restantes áreas, a juegos infantiles y espacios con mesas y sillas para los visitantes, y un área verde. Los limites del área verde son: el área de la alberca, una diagonal del cuadrado, y un cuarto de circulo con centro en el vértice B. Determina la cantidad de pasto en rollo que se debe comprar para colocar en dicha área verde.

Pasos para resolverlo:

1) Sacar el área del semicírculo:

A = π × r² 

                          

A= (3.1416....* (35 m)² ) = 3 848.46 m²

A= 3 848.46 m²/2 = 1 924.23 m²

2) Sacar el área de la 8va. parte del circulo:

                                                                 A = π × r² 

A= (3.1416....* (70 m)² ) = 15 393,85 m²

A= 15 393,85 m²/8 = 1 924.23 m²

3) Sacar el área del triángulo inscrito en el semicírculo:

                                                            A = (b × h) / 2 

                                                               A= (70 m * 35 m) /2 = 1 225 m²

4) Restar al semicírculo el área del triángulo:

1 924.23 m² -1 225 m² = 699.23 m²

^{5) Dividir ese resultado entre dos:}

                                                           699.23 m² /2 = 349.615 m²

6) Restar ese resultado al área sacada en el punto 2:

                                                1 924.23 m²- 349.615 m²= 1 574. 61 m²

Y ese es la cantidad de pasto del área verde.

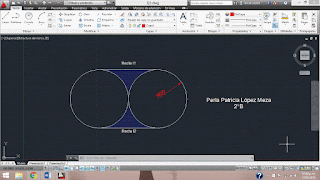
Problema 1. En la figura, las dos circunferencias tienen un radio de 20 cm cada una y son tangentes entre si, las rectas l1 y l2 son tangentes a las circunferencias como se observa en la figura. Determina el área sombreada.

Pasos:

1) Sacar el área de uno de los círculos;

                                                                                    A = π × r² 

A= (3.1416....* (20 cm)² ) = 1256.64  cm²

2) Si observamos, el área sombreada es un cuadrado, y dado que el radio que nos proporcionan es 20 cm,  la medida de un lado del cuadrado será 40 cm, entonces:

                                                                    A= (40 cm) (40 cm) = 1 600  cm²

3) Al área del cuadrado restar la del circulo:

                                                  A= 1 600 cm² -1256.64  cm²= 343.36 cm²

Problema 2. El área del cuadrado menor es 81 in² . Determina el área del circulo y del cuadrado mayor.

Pasos:

1) Sacar la medida de la diagonal del cuadrado menor, mediante el teorema de Pitágoras:

c = √ a²+b²

c= √ 9²+9²

c = √ 162

c =12.72 in

2) Ese resultado es nuestro diámetro, por lo tanto nuestro radio es la mitad, de aquí sacamos el área del circulo:

                                                                 A = π × r² 

A= (3.1416....* (6.36 in)² ) = 127.23  in²

3) De el área  obtenida le restamos el área del cuadrado menor 80 in² dándonos un resultado de 47.23 in² . Esa es el área de la parte sombreada del circulo.

4) Observamos que el diámetro del circulo es nuestra media de uno de los lados del cuadrado mayor, así que: 12.72 in * 12.72 in = 161.79 in²

5) Restamos 161.79 in²- 127.23  in² =  34.56 in² . Siendo este resultado el área sombreada del cuadrado mayor.

Figuras en AutoCAD

Ángulos entre paralelas

Ángulos entre paralelas

Al intersectar una paralela por una secante, se forman los siguientes tipos de ángulos:

Ángulos correspondientes:

 Son los que están al mismo lado de las paralelas y al mismo lado de la transversal.

Ángulos alternos internos:

Son los que están entre las paralelas a distinto lado de ellas y a distinto lado de la transversal.

Ángulos alternos externos:

 Son los que "fuera" de las paralelas a distinto lado de ellas y a distinto lado de la transversal. Las propiedades fundamentales de los ángulos entre paralelas son:

1.     Los ángulos correspondientes son iguales entre sí.

Los ángulos 1 y 2 son iguales

2. Los ángulos alternos internos son iguales entre sí.

 Los ángulos 2 y 3 son iguales.

3. Los ángulos alternos externos son iguales entre sí.

Los ángulos 1 y 4 son iguales.

Puntos notables en el triángulo

Puntos notables en el triángulo

Baricentro

El baricentro (o centroide) G es el punto donde concurren las tres medianas del triángulo.

Las medianas (m_a, m_b y m_c) son los segmentos que unen uno de sus vértices con el centro del costado opuesto.

Se cumple la siguiente propiedad: la distancia entre el baricentro y su vértice correspondiente es el doble de la distancia entre el baricentro y el lado opuesto. Es decir, la distancia del centroide a cada vértice es de 2/3 la longitud de cada mediana.

Ortocentro

Las alturas son las rectas perpendiculares trazadas desde cada vértice al lado opuesto o a su prolongación.

Las tres alturas de un triángulo ABC se cortan en un punto H, llamado ortocentro del triángulo.

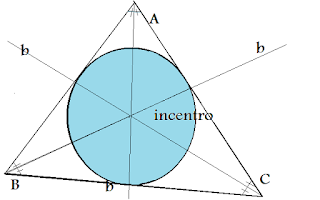
Incentro

El incentro (I) es la intersección de las tres bisectrices del triángulo.

Las bisectrices de un triángulo (B_a, B_b y B_c) son los tres segmentos que, dividiendo cada uno de sus tres ángulos en dos partes iguales, termina en el correspondiente lado opuesto.        

El incentro (I) es el centro de la circunferencia inscrita en el triángulo.

Circuncentro

El circuncentro de un triángulo es el punto donde se cortan las mediatrices de los lados. Dicho punto equidista de los vértices y, por lo tanto, es el centro de la circunferencia circunscrita al triángulo.

Figuras en AutoCAD

Propiedades de las Figuras Planas

Hola, aquí les dejo la presentación que contiene algunas propiedades de las figuras planas mas comunes.

Propiedades de las figuras planas from Perla Meza

Razón Áurea

La armonía del rectángulo áureo.

Temas

-Introducción

-Razón áurea

-Aplicaciones de la razón áurea.

La geometría es una de las áreas matemáticas más empleadas en la actualidad.

Existen tres números de gran importancia en las matemáticas y que  nombramos con una letra. Estos números son:

·          El número designado con la letra griega  = 3,14159....(Pi) que relaciona la longitud de la circunferencia con su diámetro ( Longitud = 2..radio= .diámetro).

·          El número e = 2´71828......, inicial del apellido de su descubridor Leonhard Euler (matemático suizo del siglo XVIII) que aparece como límite de la sucesión de término general .

·          El número designado con letra griega = 1,61803... (Fi), llamado número de oro y que es la inicial del nombre del escultor griego Fidias que lo tuvo presente en sus obras.

Los tres números tienen infinitas cifras decimales y no son periódicos (sus cifras decimales no se repiten periódicamente). A estos números se les llama irracionales

Desde el tiempo de los egipcios, muchas veces las construcciones fueron creadas con base en relaciones geométricas que los científicos de aquella época fueron capaces de idear y desarrollar.

Uno de los grandes hallazgos de esa época es el denominado número de oro o número áureo (golden number en inglés). Desde su determinación, han aparecido de este número muchas demostraciones

A continuación abordaremos la concepción natural de perfección en la belleza de la naturaleza y su relación con el número áureo. También veremos las realizaciones de esta proporción que pueden observarse en diversos campos de la ciencia.

Razón Áurea

La razón áurea, también llamada razón dorada, número de oro, o divina proporción, es un concepto matemático que ha interesado y entusiasmado a personas de áreas tan diversas como la biología, por un lado, y la arquitectura y la pintura, por otro.

Pitágoras en el siglo VI a. C. observó que toda armonía dependía de una proporción, de una relación numérica: “Todo está ordenado de acuerdo a números” La palabra cosmos, a él atribuida, significa “orden”. El concepto de proporción, es en lógica como en estética, uno de los más importantes y más difíciles de definir con precisión.

Llamamos proporción a la igualdad de dos razones, definiendo la razón como el cociente entre dos números enteros.

Llamamos rectángulo al cuadrilátero que tiene sus lados opuestos congruentes, y sus ángulos interiores rectos. Si nos encontramos frente a dos rectángulos de tamaño diferente, la manera de distinguir uno de otro es por la razón entre el lado mayor y el lado menor.

Según Euclides  en su Libro VI de los Elementos de Geometría, escrito hace aproximadamente 2300 años:

“Decimos que una línea recta está dividida en razón media y extrema cuando toda la línea es al segmento más grande lo que el segmento más grande es al más pequeño”.

Dicho de otra manera, la recta de longitud a + b está dividida en razón media y extrema en dos segmentos de longitudes a y b si a + b / a = a / b. Se puede demuestra que en este caso a b = φ y que φ = ( 1 + √ 5 ) / 2 = 1.61803398 . . .

La razón aurea es un número muy atractivo que está relacionado con varios objetos matemáticos, como los números de Fibonacci y algunas construcciones geométricas. Una de ellas es el rectángulo dorado: aquél cuyos lados están en razón φ a 1, es decir, si a y b son las longitudes de los lados del rectángulo y a es mayor que b, entonces a/b = φ.

La sorprendente belleza de un número irracional.

El número áureo pertenece al conjunto del número irracional, esto es, aquellos que no pueden expresarse como cociente de dos número enteros. Por ejemplo, la raíz cuadrada de dos es irracional -un descubrimiento que incomodó de tal modo a los pitagóricos que lo ocultaron al mundo-. En nuestro caso, el número áureo lo podemos computar con una calculadora si seguimos estas sencillas instrucciones: primero, calculamos la raíz cuadrada de 5; luego sumamos 1 al resultado y el total lo dividimos por 2. Si sabemos programar un ordenador, podemos intentar batir el récord del mayor número de decimales calculados: en el año 2000 y con menos de 3 horas de computación, se encontraron los primeros 1.500 millones de cifras decimales.

De Φ derivan otros patrones de la naturaleza como el ángulo áureo que resulta de representar la proporción aurea en un círculo de este modo Φ describe el orden de las hojas de una palmera, de las escamas de una piña de las semillas en un girasol, la distribución de las hojas alrededor del tallo, entre otros fenómenos. Por otra parte el matemático Leonardo de Pisa conocido como Fibonacci estableció la siguiente sucesión de números: 1, 1, 2, 3, 8, 13, 21, 34, 55, 89,… La sucesión de Fibonacci es muy simple, en ella cada término es la suma de los dos anteriores. Si en esta sucesión dividimos el segundo término por su antecesor y el tercer termino por su antecesor y así sucesivamente, observaremos que el resultado de estas divisiones se acerca cada vez más al número de oro 1.168…). Es así como se demuestra que el límite de estos cocientes cuando la sucesión de Fibonacci tiende a infinito es el número de oro.

1/1=1

2/1=2

3/2=1.5

5/3=1.666

8/5=1.6

13/8=1.625

21/13=1.615

34/21=1.619

55/34=1.617

89/55=1,618 …

Entre la infinidad de aproximaciones de φ, como son 1.61803 y 1.61813 o simplemente 1.618, sólo φ, con su expansión decimal infinita, se distingue por sus notables propiedades matemáticas.

Esta sucesión está presente, en la reproducción de los conejos, en la reproducción de las abejas, en los brotes de infinidad de plantas, así como en muchos fenómenos más de la naturaleza. Otra fenómeno importante donde se encuentra el número dorado es la espiral logarítmica, la cual se genera al de dividir un rectángulo áureo (rectángulo con las proporciones del número Φ) en otros rectángulos dorados de manera infinitamente, en los cuales se forma dicha espiral. Esta espiral se manifiesta en la disposición de las semillas en numerosas flores y frutos, en la orejas del ser humano, en las conchas de moluscos y caracoles, y en escala mucho mayor en los brazos en espiral de las galaxias.

Por ejemplo en los anillos de Cassini del planeta Saturno podemos encontrar la relación Phi, que se muestra a continuación.

La serie de Fibonacci es uno de los conjuntos de números que aparecen muy frecuentemente dentro de la naturaleza. Por ejemplo, el número de pétalos de muchísimas flores es un número de la serie. En crecimiento de plantas, el número de ramas que se van obteniendo a medida que el árbol crece es usualmente un número perteneciente a la serie 6. Otro ejemplo típico es el cono de pino (o piña de pino). Un cono de pino se puede pensar como un conjunto de espirales que se van retorciendo hasta llegar a unirse en un punto que es el que se une al tallo. Hay ocho espirales en la dirección de las manecillas del reloj, mientras que hay 13 que se acercan más rápidamente a la punta en contra de las manecillas del reloj (situación muy similar se puede observar en una piña o en el girasol o en la coliflor). La frecuencia con la que números pertenecientes a la serie de Fibonacci se manifiestan dentro de muchos objetos o situaciones en la naturaleza parecen indicar que hay algo intrínseco y óptimo que la naturaleza ha desarrollado

En las hojas de ciertas plantas, apreciamos también esto, en una hoja de la planta, el número de hojas que hay entre una hoja y otra que este justo perpendicularmente encima de la misma, este número de hojas como el número de vueltas que da al tallo, está en la sucesión de Fibonacci.

En las semillas de las plantas, la semilla es circular, si dividimos sus grados ( 360º)entre Phi, aproximadamente da 222,5º, si ahora restamos 222,5º a los 360º de un círculo completo obtenemos 137,5º, que es el ángulo de separación entre las raíces que nacen consecutivamente. Es gracias a esto, de una manera natural, que no se amontonan unas sobre otras y aprovechan mejor el terreno.

La concha del nautilius: la concha de este caracol tiene una espiral, pero esa espiral es una espiral áurea, que se obtiene de la siguiente forma: a través de un rectángulo áureo (el lado mayor entre el menor es Phi) o un triángulo áureo (triángulo isósceles cuya proporción entre un lado mayor y el menor, o el mayor entre uno menor es Phi) que se explica con un rectángulo áureo.

De alguna forma el número Phi está en la naturaleza porque la naturaleza asi lo pide, porque es la forma más elemental de organizarse y crecer a partir de dos elementos.

En el vuelo de un halcón, supongamos que se encuentra o está  justo encima de su presa.  Si efectivamente esta perpendicularmente encima, el halcón bajará haciendo una espiral áurea, y de ese modo, baja lo más rápido posible manteniendo su vista siempre sobre la presa.

Leonardo da Vinci

Hijo del notario italiano Piero da Vinci, fue educado en la casa de su abuelo paterno hasta 1469, fecha en que viajó a Florencia junto con su padre y comenzó a frecuentar el taller de Andrea del Verrocchio. En 1472 aparece inscrito en la Compagnia di San Luca, de pintores florentinos. Con su maestro, Verrocchio, adquiere el conocimiento de las diferentes técnicas artísticas; junto a él se sabe que trabajó en la ejecución del Bautismo de Cristo, actualmente conservado en la Galería de los Uffizi de Florencia. A este primer decenio corresponden obras que se enmarcan dentro del ámbito figurativo en el que se mueve Leonardo, con influencias de Verrocchio, Lorenzo di Credi, Pollaiolo, o el joven Botticelli. De este momento, además de numerosos dibujos, se conserva La Anunciación, en la Galería de los Uffizi; el Retrato de Ginebra Benci, en la National Gallery de Washington; la Virgen de Benois, en el Ermitage de Leningrado; La Virgen del clavel, de Munich; el San Jerónimo, en la Pinacoteca Vaticana de Roma; y la Adoración de los Magos, en la Galería de los Uffizi de Florencia, encargada en 1481 por los monjes de San Donato en Scopeto y que quedó sin terminar debido a su viaje a Milán.

Leonardo da Vinci, en su cuadro de la Gioconda utilizó rectángulos áureos para plasmar el rostro de Mona Lisa. Se pueden localizar muchos detalles de su cara, observando por empezar, que la misma se encuadra en un rectángulo áureo.

 La construcción del rostro de la Gioconda pintada por Leonardo de Vinci es similar a la construcción de la espiral áurea del nautilo.

Pero Leonardo no solo las utilizó en la cara de la Mona Lisa, también la utilizó en muchas otras obras reprentando la belleza de la proporción áurea sobre el cuerpo humano. Unas proporciones armoniosas para el cuerpo, que estudiaron antes los griegos y romanos, las plasmó en este dibujo Leonardo da Vinci. Sirvió para ilustrar el libro La Divina Proporción de Luca Pacioli.

En el siglo XV el monje Luca Pacioli, llamó “la divina proporción” dando un porqué. De acuerdo a él, phi “tiene una correspondencia con la santísima trinidad; es decir, así como hay una misma sustancia entre tres personas, de igual modo una misma proporción se encontrará siempre entre tres términos, y nunca de más o menos”.

Resulta que el cociente entre la altura del hombre (lado del cuadrado) y la distancia del ombligo a la punta de la mano (radio de la circunferencia) es el número áureo.

Muchos artistas de la actualidad aún siguen escondiendo la curiosa proporción divina en muchos de sus cuadros, fotografía, aunque no lo podamos ver a simple vista. Tal como es en el caso de Cartier-Bresson en la que como vemos en la imagen, utiliza la espiral para dar un efecto armonioso y enrevesado a su fotografía titulada "Blanco y Negro".

También el pintor holandés Piet Mondrian, fundador del neoplasticismo, (corriente artística que proponía despojar al arte de todo elemento accesorio) utilizó la proporción áurea en la geometría de sus obras.

Joaquín Torres García (pintor contemporáneo) también utiliza la simetría del número áureo para representar muchas de sus pinturas como la de "Construcción" y "Guavich":

Johannes Kepler (1571-1630), descubrió la naturaleza elíptica de las órbitas de los planetas alrededor del sol, mencionó también la “Divina Proporción", diciendo esto acerca de ella: "La geometría tiene dos grandes tesoros: uno es el teorema de Pitágoras; el otro, la división de una línea entre el extremo y su proporcional. El primero lo podemos comparar a una medida de oro; el segundo lo debemos denominar una joya preciosa."

En la música

El compositor húngaro Bela Bartok y el francés Olivier Messiaen utilizaron esta serie para determinar la duración de las notas de algunas de sus obras.

El compositor mexicano Silvestre Revueltas (1899-1945) utilizó también el número áureo en su obra Alcancías, para organizar las partes (unidades formales).

También encontramos las proporciones del rectángulo áureo y sus secciones en Nueva York, en el Edificio de la O.N.U.

En la actualidad, la divina proporción se puede ver en multitud de diseños. El más conocido y difundido es en el formato de la mayoría de las tarjetas de crédito, asi como en los estadios de fútbol, tenis, e inclusive si abres tu cartera, un billete tiene esta proporción.

A lo largo de este tema hemos visto que artistas, ingenieros, fotógrafos, arquitectos y diseñadores hacen uso de la razón áurea ya que se ha creído que se puede para impartir armonía y estética a sus creaciones. Se piensa que los productos que son diseñados con la Razón Áurea son más atractivos a la vista del usuario, es por ello que los profesionales de estas áreas hagan uso de los fundamentos y aplicaciones de este número. Sin embargo esto no aplica en todo lo que nos rodea, no se sabe si solo es un mito, pero no cabe duda que sería difícil quitar o desmentir una creencia de muchos años de antigüedad.

Encontrar orden matemático en un universo de aparente belleza divina es realmente sorprendente, pero no es una prueba de algún diseñador inteligente, pero comúnmente al ver estos diseños en la naturaleza creemos en la existencia de alguien superior. Los apologistas y teólogos modernos afirman la existencia de un Dios.

¿Y tú crees que sea cierto que la razón áurea da armonía?

Funciones Matemáticas

Rectángulo Áureo

El número áureo es el valor numérico de la proporción que guardan entre sí dos segmentos de recta a y b que cumplen la siguiente relación:

 

 Este valor numérico nos debe arrojar el siguiente resultado:

  

  

Fue descubierto en la antigüedad, y puede encontrarse tanto en figuras geométricas, como en la naturaleza. 

El descubrimiento de este número se atribuye a la escuela Pitagórica, de hecho los pitagóricos utilizaban como símbolo la estrella de cinco puntas, en la que aparecen distintas razones áureas.A menudo se le atribuye un carácter estético especial a los objetos que contienen este número, y es posible encontrar esta relación en diversas obras de la arquitectura u el arte.

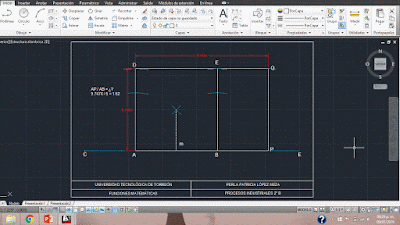
Para la construcción de un Rectángulo Áureo en AutoCAD, seguimos los siguientes pasos:

Primero ponemos "Nuevo" y seleccionamos la hija de Acad, luego 

trazamos una linea, luego seleccionamos la opción de "Circulo, Radio" y el centro será como a la tercera parte de nuestra linea, siendo nuestro punto A, donde la medida del radio es la altura que deseemos de nuestro rectángulo. La primera intersección con nuestra linea será el punto C, la segunda intersección es el punto B, así pues volvemos a trazar un circulo con el mismo radio, pero esta vez como centro el punto B, después, trazamos una linea que vaya desde el punto A hasta la circunferencia, a un ángulo de 90° donde tendremos el punto D, del mismo modo trazamos otra linea desde el punto B obteniendo el punto E, después,unimos A y B luego D y E, obteniendo un cuadrado. Lo siguiente que necesitamos es marcar el punto medio (m) del segmento AB. Luego hacemos un circulo desde m con un radio que vaya desde m hasta E, donde se cruce con nuestra primera linea será P, de aquí será nuestro centro para un nuevo circulo con un radio de la medida que tenga la altura de nuestro cuadrado. Casi para finalizar trazamos otra linea de P a 90° hasta la circunferencia, este punto será Q. Finalmente, unimos Q con E.

Para verificar que nuestro rectángulo y cuadrado son áureos, dividimos la medida del largo del rectángulo entre la medida de un lado del cuadrado, esta nos debe dar un valor cercano a "1.618033..." .

He aquí el enlace del archivo:

https://drive.google.com/open?id=0BxvXw2ck5sFtVDVQZUxMUXcxQWc

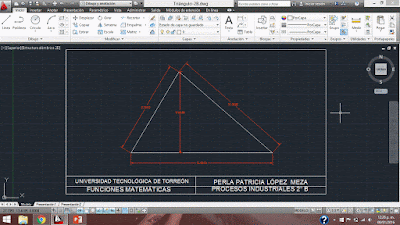
                                    Triángulo escaleno en AutoCAD

Uno de los elementos más importantes de un triángulo es su altura, de aquí partiremos primero donde tenemos tres medidas de sus lados, que son 8 cm, 10.5 cm y 12 cm, sin embargo, no contamos con su altura y para esto vamos a usar la Fórmula de Herón, siendo:

A= √s(s-a)(s-b)(s-c) , donde s= (a+b+c)/2 →  s= 15.25 , sustituyendo tenemos que 

A= √15.25 (15.25-8)(15.25-10.5)(15.25-12) dando un resultado de 41.3136  cm², 

por lo tanto la fórmula para el área de un triángulo dice que A= b*h / 2, obtenemos que

h= 2A/b, siendo así: h=82.6272 cm²/12 cm = 6.8856 cm

Para confirmar este resultado, trazaremos nuestro triángulo en AutoCAD. Primero abrimos AutoCAD, luego le ponemos en "Nuevo" y escogemos la opción de Acad, ya en nuestra nueva hoja trazamos una linea de 12 cm, luego seleccionamos la opción de "Circulo, Radio" y ponemos nuestro centro en el primer punto de nuestra linea y le damos un valor de radio de 8 cm, volvemos a poner el comando de "Circulo, Radio" y esta vez seleccionamos el segundo punto de la linea, con un radio de 10.5 cm, después unimos los puntos con la intersección de las circunferencias. Para ver del valor de la altura, seleccionamos la opción de medir y seleccionamos desde la intersección hasta nuestra linea de 12 cm, dándonos un valor de 6.8856 cm.

A continuación se muestra el enlace donde se encuentra el archivo:

https://drive.google.com/open?id=0BxvXw2ck5sFtME01X2dhUnBrTG8